皆さんこんにちは、東大BKKコンテンツ編集部です!
| 京大、阪大、早稲田大、筑波大などトップ大学に合格者を輩出する偏差値UP学習術とは? |
|---|
 |
|
【今だけ5,000円→無料!】 無料で読める電子書籍「偏差値UP学習術25選」 ・苦手科目を克服しようとすると成績が下がる理由 ・勉強しても成績が伸びなくなるブレーキの存在 ・1日5分で効率の良い勉強を習慣にする方法 などなど。 受験生であれば、ついつい気になる受験の仕組みを、プロが解説付きの電子書籍で徹底解説! 受講料は無料で受けられるので、受験生にも話題に! 
京大、阪大、早稲田大、筑波大などトップ大学に合格者を輩出する受験コーチのメソットを無料の電子書籍を、今すぐ無料で読むことができます! 
※無料ですぐに読むことができます。 |
「因数分解とは?」「因数分解のやり方忘れたんだけど、分かりやすく教えて!」
こんな疑問をあなたも今持っていませんか?
この記事では因数分解をテーマに解説していきます。
因数分解のやり方をわかりやすく解説しているので、これを読めば丸わかりです!!
記事は3~5分で読み終わります。この記事が少しでも皆さんのお役に立てれば幸いです。

| 京大、阪大、早稲田大、筑波大などトップ大学に合格者を輩出する偏差値UP学習術とは? |
|---|
 |
|
【今だけ5,000円→無料!】 無料で読める電子書籍「偏差値UP学習術25選」 ・苦手科目を克服しようとすると成績が下がる理由 ・勉強しても成績が伸びなくなるブレーキの存在 ・1日5分で効率の良い勉強を習慣にする方法 などなど。 受験生であれば、ついつい気になる受験の仕組みを、プロが解説付きの電子書籍で徹底解説! 受講料は無料で受けられるので、受験生にも話題に! 
京大、阪大、早稲田大、筑波大などトップ大学に合格者を輩出する受験コーチのメソットを無料の電子書籍を、今すぐ無料で読むことができます! 
※無料ですぐに読むことができます。 |
因数分解とは
因数分解とは多項式をより簡単な多項式や単項式で表すことです。
具体的に分かりやすく説明すると、18を3×6として表現するのを因数分解といいます。
さらに数学的な内容においては、因数分解はしばしば↓のように習います。

因数分解とは
ここで一緒にしがちなのが、「展開」です。
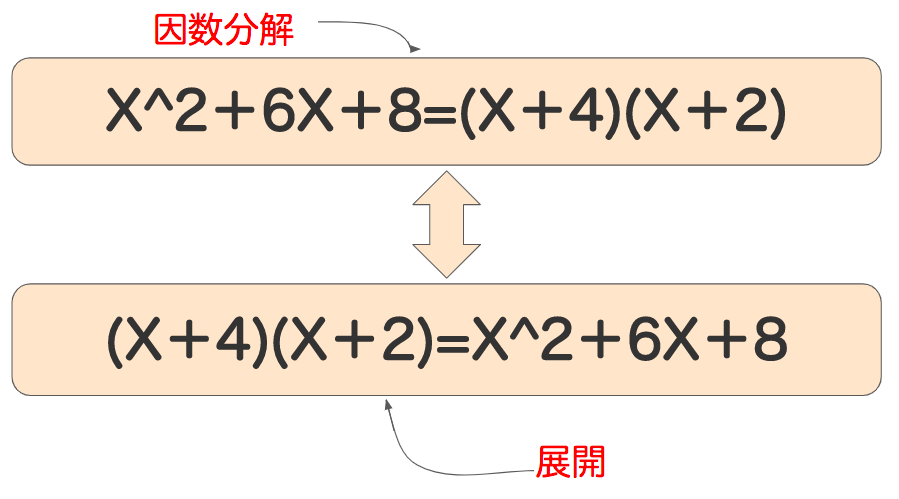
因数分解と展開
因数分解を習いたての頃は、展開と因数分解をゴッチャにしがちです。
さきほど紹介したように、因数分解は多項式を因数に分解する作業のことです。ここを忘れずにしておきましょう。

因数分解とは
さて、因数分解がどういうものかはなんとなく分かってくれたかと思います。
ここでこんな疑問が湧いてきませんか?↓↓↓
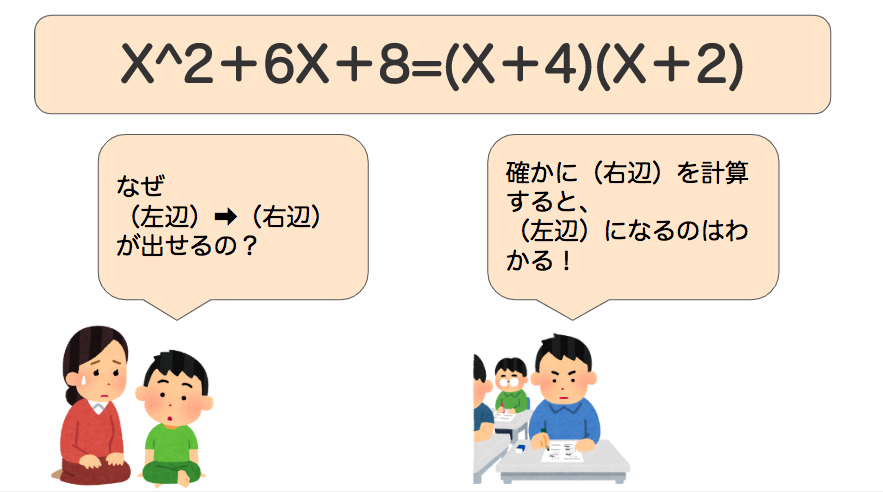
この子供が語っている通り、展開は式が与えられていればできます。
しかし、因数分解は因数分解の解き方・やり方を知っていないとできない問題なのです。
ここからは実際の因数分解の解き方を見ていきます。

因数分解の公式などを解説
先に公式を紹介します。
因数分解の二乗の公式
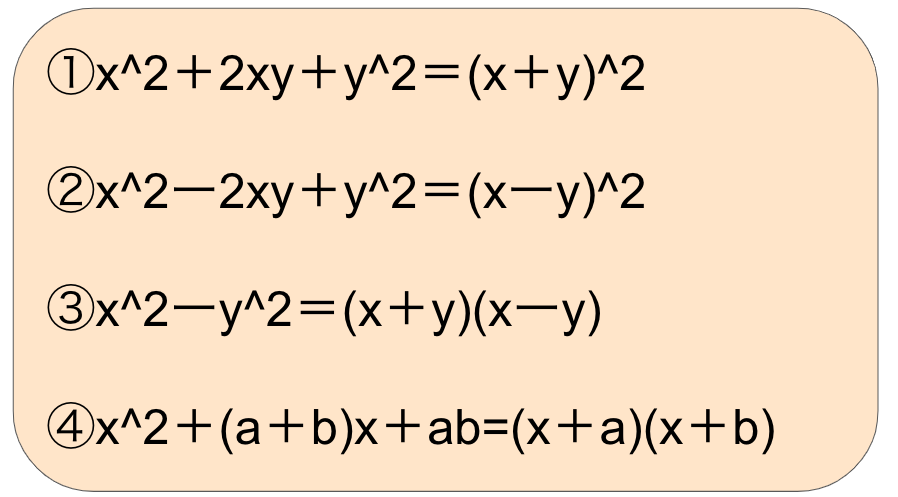
因数分解の三乗の公式
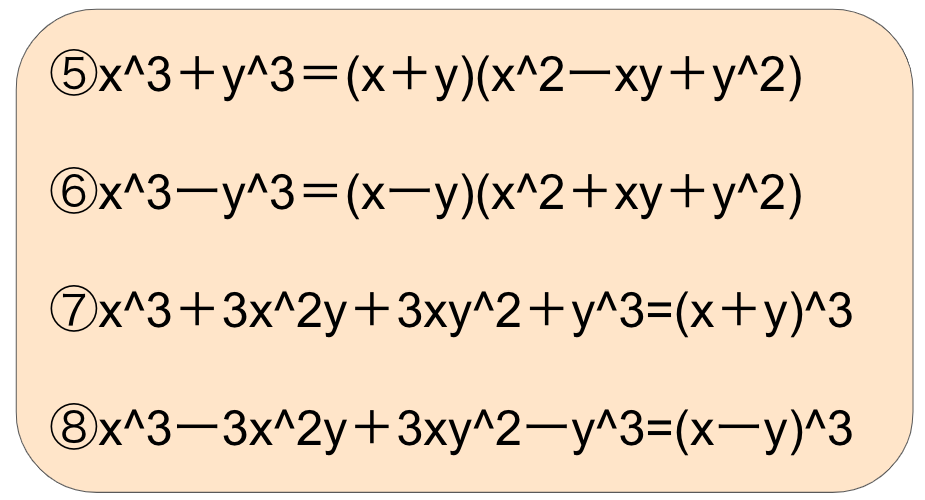
二乗も三乗もまずは公式を覚えましょう。
このあと紹介するたすきがけの問題が出来るようになるのが因数分解マスターには必要不可欠です。

因数分解の例題
具体的な因数分解の問題の解き方ですが、さきに結論を言いますと
どの公式に当てはまるか
を考えることを常にしてください。具体的には与えられた問題が先ほど紹介しました公式①〜⑧のどれに当てはまるかを考えることです。
これを踏まえて、それでは具体的な問題の例で考えていきます。
例題①:x二乗の係数が1の場合
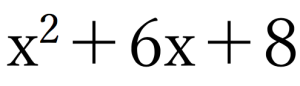
↑を因数分解せよ、という問題が出たとします。
では上記の式はどれに当てはまるでしょうか。
正解はズバリ④です。
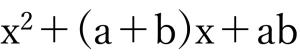
④の公式
①〜③の型でないことには気づいて欲しいです。
④だとわかれば、
- a+b=6
- ab=8
なので、それに当てはまる数字を考えると
(a,b)=(4,2)(2,4)
となります。
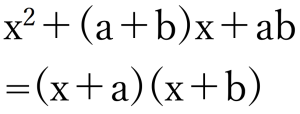
④の公式
公式より答えは、
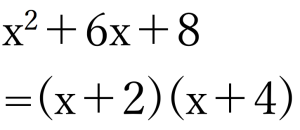
となります。
いかがでしょう。もう一度やり方の基本を振り返ると、
- 公式の型のどれに該当するか確認する
これだけです。
もう一問だけこの章では紹介しておきます。
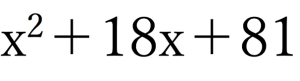
演習例題①
↑回答は記事の一番下で。
例題②:x二乗の係数が1でない場合
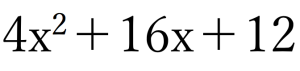
↑を因数分解せよ、という問題が出たとします。
では上記の式はどれに当てはまるでしょうか。
結論からいうと、④です。
しかし、④とは明らかに違う点がありますよね。
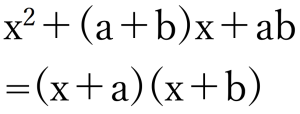
④の公式
x二乗の係数が4となっている所が公式とは違います。
ここで因数分解で大事な
- 共通因数でくくる
という概念を理解する必要があります。
今回この問題のそれぞれの項は、全て4の倍数です。つまり共通因数が4です。

どうでしょう。④の公式に見えてきませんか?
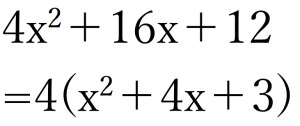
共通因数4でくくると↑、こうなるので、後は因数分解の公式を用いて
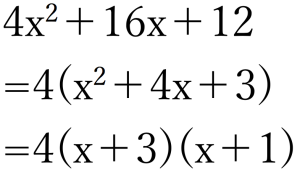
こうなりました。
それではこの形の問題を1つ紹介しておきます。回答は記事の一番下で。
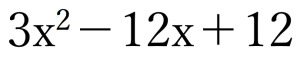
演習例題②

たすきがけの公式
残念ながら、ここまで紹介した①〜⑧までの公式では解けない因数分解の問題があります。
たすきがけの公式を理解できれば、因数分解はOKです。それでは見ていきます。
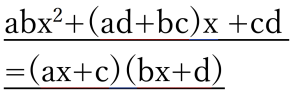
たすきがけの因数分解
何のことを言ってるかはともかく、まずは右辺を展開すると左辺になることを確認してください。
たすきがけの例題①
具体的にこのたすきがけの因数分解を利用しなければ解けない問題はこのような問題。
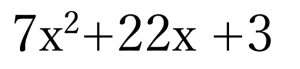
たすきがけの例題①
これまでの説明だと、↑の式は明らかに①〜④の型ではないので
- 共通因数でくくる
という作業をする必要があります。
しかし共通因数がありません。7、3は互いに素で共通因数でくくれないので、この式は①~④に当てはまらないことになります。
ここでたすきがけの因数分解を用います。
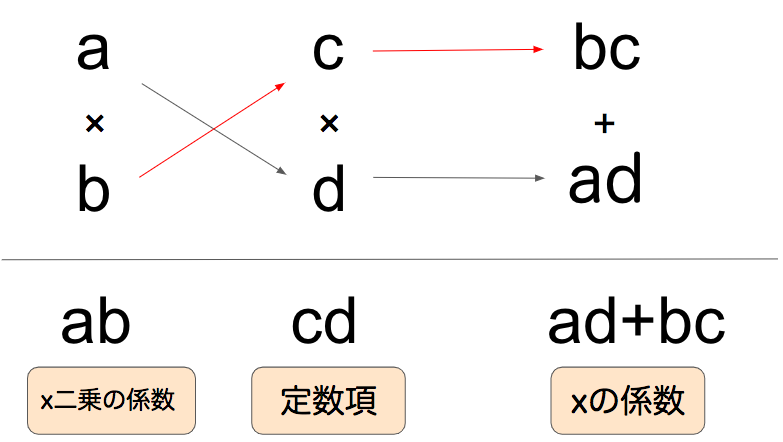
たすきがけの因数分解
- 二乗の係数をabに分解
- 定数項をcdに分解
- うまく掛け合わせてad+bc(←xの係数)を作る
これがたすきがけの極意です。
具体的に
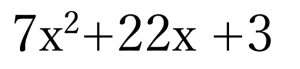
この問題でやってみます。
- 二乗の係数をabに分解
→(1,7)に分解 - 定数項をcdに分解
→(1,3) に分解 - うまく掛け合わせてad+bc(←xの係数)を作る
→7×3+1×1=22
以上を
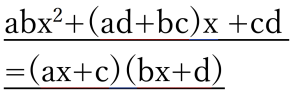
たすきがけの因数分解の公式
この公式を参考に因数分解すると、
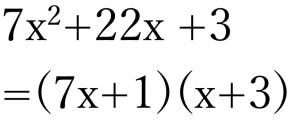
こうなります。まとめると↓こうですね。
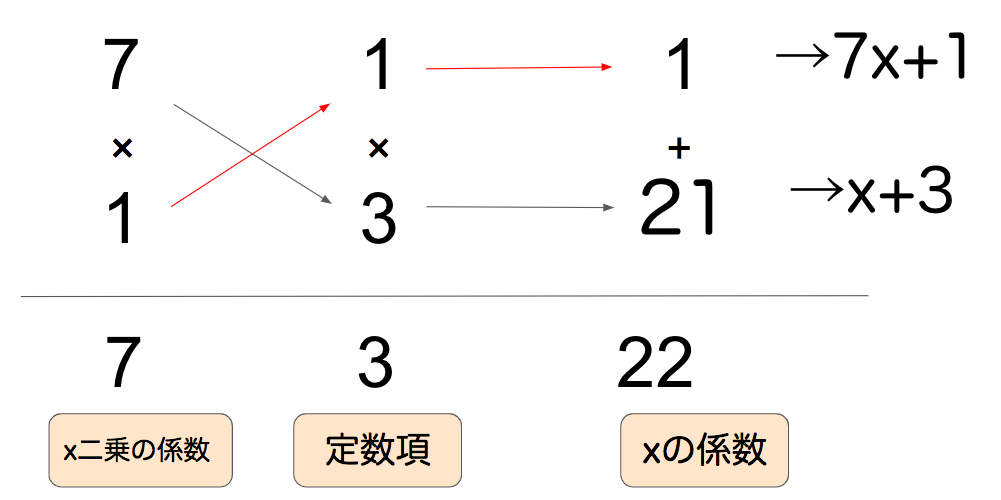
確認用
ここまでをまとめます。
- ①〜④の公式の型かどうか判別する
- 共通因数でくくれるか確認する
- 共通因数でくくれない場合は、たすきがけの因数分解をする
この3ステップをすれば、因数分解の問題で解けない問題はありません。
しかし、今こんなことを考えている人がいると思います。

大丈夫です。そんな心配はいりません。
因数分解のコツは答えを展開してみることです。
例えば上の式であれば、
- (7x+1)(x+3)
- (7x+3)(x+1)
かのどちらかで悩んでしまう人います。しかし問題ありません。
展開した式と問題の式が間違っていれば、因数分解が間違っていたことが分かります。

因数分解の確認
逆に考えてみると、展開して検算をしていれば、因数分解は間違う可能性が0なのです。
それではもう一問だけ同じパターンの問題を。
たすきがけの例題②
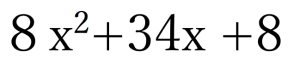
たすきがけの例題②
- ①〜④の公式の型かどうか判別する
- 共通因数でくくれるか確認する
- 共通因数でくくれない場合は、たすきがけの因数分解をする
とにかく因数分解はこれです。
まず、①〜④の公式の型ではないですね。
次に共通因数ですが、今回は2が共通因数となっていることに気づいたでしょうか。
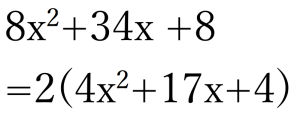
共通因数2でくくる
そして手順3のたすきがけです。
4は(1,4)または(2,2)の2つの分け方があります。しかし今回の場合、ここで掛け合わせて17というものを作ることを考えると、、、
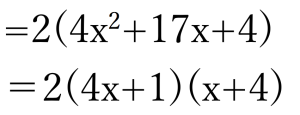
こうですね。確認用に以下のスライドもどうぞ。
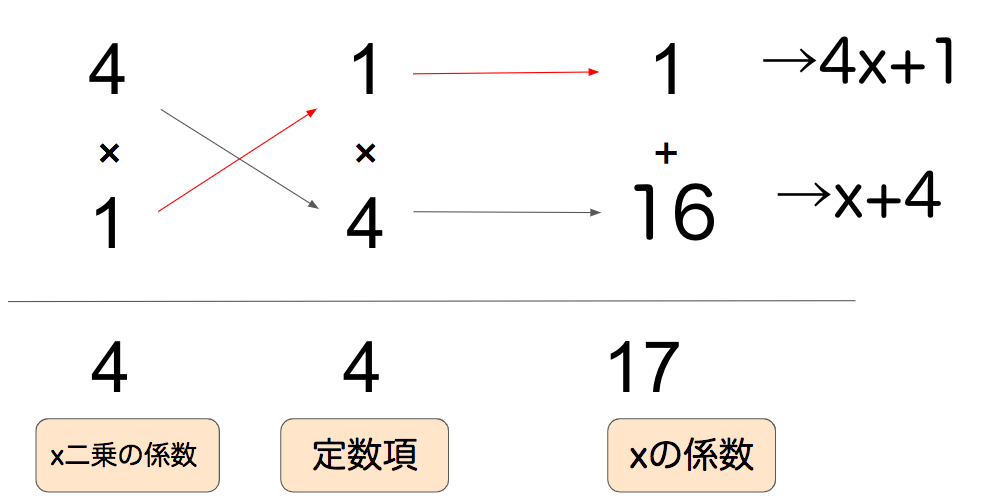
確認用
たすきがけの問題も練習用問題を一問載せておきます。回答は記事下で、
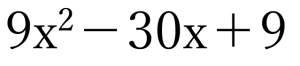
演習例題③

因数分解の3乗など難しめの問題
ここまで二次関数、公式①〜④を用いたものしか紹介していないので、3乗の問題についても扱っていきます。
しかし基本は全く同じなので、身構える必要は0です。
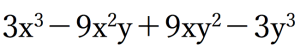
このような問題が出てきたら、
- ⑤〜⑧の公式の型かどうか判別する
- 共通因数でくくれるか確認する
- 共通因数でくくれない場合は、たすきがけの因数分解をする
これだけです。二乗の場合と変わりません。
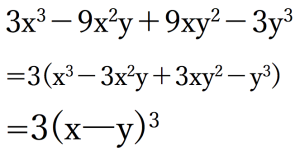
瞬殺ですね。3乗の問題も2乗の問題も公式を覚えておくことが大切です。

因数分解の問題について
今回扱ったのは因数分解の基礎中の基礎です。
因数分解はまずは公式をはじめとした基礎的問題を攻略し、その後に難しい応用問題を解いていく必要があります。
そしてその応用問題についてはパターンを1つ1つ学んでいくしか方法はありません。因数分解は展開とは違って、やり方を分かっていなければできない問題なのです。
ちゃんと真面目に因数分解を学びたいという人は、ぜひ参考書を1冊買って学んでみましょう。
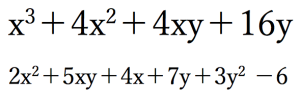
この記事を読んだだけでは解けない因数分解の問題

因数分解を使った思考
ここからは数学の話題ではありません。コラムだと思ってお読みください。
因数分解はもちろん数学の問題なのですが、この考え方は生活の色々なことに活用することができます。
因数分解のやっていることは
- 1つの事象を複数の簡単な事象に分解する
ということです。
この考え方を活用すると、身近な複雑に見える事象も紐解いて見えるようになります。
例えば、この記事を読んでくださっているということで、「勉強の成績」についても因数分解の考え方を活用できます。
【成績を伸ばす】ためには何をすればいいか。ズバリBKKが出す成績アップの方程式はこうです。
【成績アップ=長い勉強時間×質】

成績アップの方程式
受験生が1日2時間しか勉強しないのでは論外ですし、かといって1日10時間で英単語50個しか覚えれないような勉強もダメです。
- 長い勉強時間
- 高い質(=集中力)での勉強
2つのどちらがかけていても、成績アップには繋がりにくいということです。
「成績を上げたい!成績をあげたい!」と考えている人はぜひ↑この考えを知っておきましょう。
まとめると、
世の中に溢れている事象をどの程度抽象的に見れるかで、因数分解できる能力というものは変わってきます。
学生の皆さんであれば、部活なども例に取ってみるといいですね。部活で試合に勝つために必要だと思うことをピックアップしてみてください。
- 毎日の練習
だけしか思いつかない人は、そのスポーツを因数分解する能力がまだ低いかもしれません。
- 毎日の練習
- 練習のやり方の改善
- プロ選手の動画を参考にする
- 食事に気をつける
- 精神的に強くなる
などなど、勝つために必要なことをいくつも思いつく人の方が往々にして強いですね。勝つために必要なことを知っているので、それを実践するだけです。
皆さんもぜひ勉強や部活に限らず、世の中に溢れている物事を因数分解してみる力をつけていきましょう。
【本質】を見抜く力はここにあります。

まとめ
今回は因数分解をテーマに解説してきました。
今回取り扱ったのは基礎の基礎です。
また、因数分解は生活の色々な所に応用できるので、ぜひ考え方だけは覚えておいてください!
例題回答
演習例題①
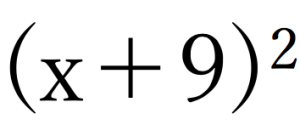
演習例題②
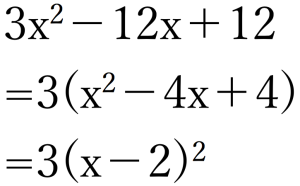
演習例題③
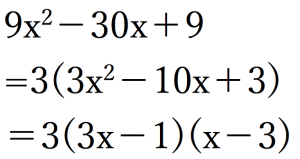
RELATED
| 京大、阪大、早稲田大、筑波大などトップ大学に合格者を輩出する偏差値UP学習術とは? |
|---|
 |
|
【今だけ5,000円→無料!】 無料で読める電子書籍「偏差値UP学習術25選」 ・苦手科目を克服しようとすると成績が下がる理由 ・勉強しても成績が伸びなくなるブレーキの存在 ・1日5分で効率の良い勉強を習慣にする方法 などなど。 受験生であれば、ついつい気になる受験の仕組みを、プロが解説付きの電子書籍で徹底解説! 受講料は無料で受けられるので、受験生にも話題に! 
京大、阪大、早稲田大、筑波大などトップ大学に合格者を輩出する受験コーチのメソットを無料の電子書籍を、今すぐ無料で読むことができます! 
※無料ですぐに読むことができます。 |